【三年26】专题20不等式选讲
【2022年全国甲卷】
1.已知a,b,c均为正数,且![]() ,证明:
,证明:
(1)![]() ;
;
(2)若![]() ,则
,则![]() .
.
【答案】(1)见解析
(2)见解析
【分析】(1)方法一:根据![]() ,利用柯西不等式即可得证;
,利用柯西不等式即可得证;
(2)由(1)结合已知可得![]() ,即可得到
,即可得到![]() ,再根据权方和不等式即可得证.
,再根据权方和不等式即可得证.
【详解】(1)[方法一]:【最优解】柯西不等式
由柯西不等式有![]() ,
,
所以![]() ,当且仅当
,当且仅当![]() 时,取等号,所以
时,取等号,所以![]() .
.
[方法二]:基本不等式
由![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
当且仅当![]() 时,取等号,所以
时,取等号,所以![]() .
.
(2)证明:因为![]() ,
,![]() ,
,![]() ,
,![]() ,由(1)得
,由(1)得![]() ,
,
即![]() ,所以
,所以![]() ,
,
由权方和不等式知![]() ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 时取等号,
时取等号,
所以![]() .
.
【点睛】(1)方法一:利用柯西不等式证明,简洁高效,是该题的最优解;
方法二:对于柯西不等式不作为必须掌握内容的地区同学,采用基本不等式累加,也是不错的方法.
【2022年全国乙卷】
2.已知a,b,c都是正数,且![]() ,证明:
,证明:
(1)![]() ;
;
(2)![]() ;
;
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)利用三元均值不等式即可证明;
(2)利用基本不等式及不等式的性质证明即可.
【详解】(1)证明:因为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
即![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
(2)证明:因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以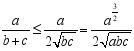 ,
,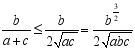 ,
,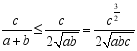
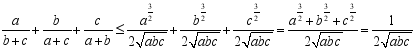
当且仅当![]() 时取等号.
时取等号.
【2021年甲卷文科】
3.已知函数![]() .
.
(1)画出![]() 和
和![]() 的图像;
的图像;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)图像见解析;(2)![]()
【分析】(1)分段去绝对值即可画出图像;
(2)根据函数图像数形结和可得需将![]() 向左平移可满足同角,求得
向左平移可满足同角,求得![]() 过
过![]() 时
时![]() 的值可求.
的值可求.
【详解】(1)可得![]() ,画出图像如下:
,画出图像如下:
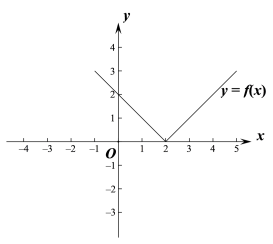
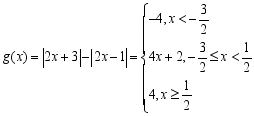 ,画出函数图像如下:
,画出函数图像如下:

(2)![]() ,
,
如图,在同一个坐标系里画出![]() 图像,
图像,
![]() 是
是![]() 平移了
平移了![]() 个单位得到,
个单位得到,
则要使![]() ,需将
,需将![]() 向左平移,即
向左平移,即![]() ,
,
当![]() 过
过![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
则数形结合可得需至少将![]() 向左平移
向左平移![]() 个单位,
个单位,![]() .
.

【点睛】关键点睛:本题考查绝对值不等式的恒成立问题,解题的关键是根据函数图像数形结合求解.
【2021年乙卷文科】
4.已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)![]() .(2)
.(2)![]() .
.
【分析】(1)利用绝对值的几何意义求得不等式的解集.
(2)利用绝对值不等式化简![]() ,由此求得
,由此求得![]() 的取值范围.
的取值范围.
【详解】(1)[方法一]:绝对值的几何意义法
当![]() 时,
时,![]() ,
,![]() 表示数轴上的点到
表示数轴上的点到![]() 和
和![]() 的距离之和,
的距离之和,
则![]() 表示数轴上的点到
表示数轴上的点到![]() 和
和![]() 的距离之和不小于
的距离之和不小于![]() ,
,
当![]() 或
或![]() 时所对应的数轴上的点到
时所对应的数轴上的点到![]() 所对应的点距离之和等于6,
所对应的点距离之和等于6,
∴数轴上到![]() 所对应的点距离之和等于大于等于6得到所对应的坐标的范围是
所对应的点距离之和等于大于等于6得到所对应的坐标的范围是![]() 或
或![]() ,
,
所以![]() 的解集为
的解集为![]() .
.
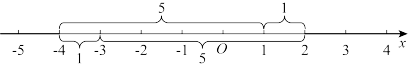
[方法二]【最优解】:零点分段求解法
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得
,解得![]() .
.
综上,![]() 的解集为
的解集为![]() .
.
(2)[方法一]:绝对值不等式的性质法求最小值
依题意![]() ,即
,即![]() 恒成立,
恒成立,
![]() ,
,
当且仅当![]() 时取等号,
时取等号,
![]() ,
,
故![]() ,
,
所以![]() 或
或![]() ,
,
解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.
[方法二]【最优解】:绝对值的几何意义法求最小值
由![]() 是数轴上数x表示的点到数a表示的点的距离,得
是数轴上数x表示的点到数a表示的点的距离,得![]() ,故
,故![]() ,下同解法一.
,下同解法一.
[方法三]:分类讨论+分段函数法
当![]() 时,
时,
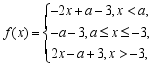
则![]() ,此时
,此时![]() ,无解.
,无解.
当![]() 时,
时,
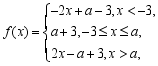
则![]() ,此时,由
,此时,由![]() 得,
得,![]() .
.
综上,a的取值范围为![]() .
.
[方法四]:函数图象法解不等式
由方法一求得![]() 后,构造两个函数
后,构造两个函数![]() 和
和![]() ,
,
即![]() 和
和![]() ,
,
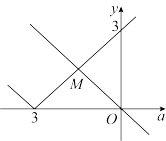
如图,两个函数的图像有且仅有一个交点![]() ,
,
由图易知![]() ,则
,则![]() .
.
【整体点评】(1)解绝对值不等式的方法有几何意义法,零点分段法.
方法一采用几何意义方法,适用于绝对值部分的系数为1的情况,
方法二使用零点分段求解法,适用于更广泛的情况,为最优解;
(2)方法一,利用绝对值不等式的性质求得![]() ,利用不等式恒成立的意义得到关于
,利用不等式恒成立的意义得到关于![]() 的不等式,然后利用绝对值的意义转化求解;
的不等式,然后利用绝对值的意义转化求解;
方法二与方法一不同的是利用绝对值的几何意义求得![]() 的最小值,最有简洁快速,为最优解法
的最小值,最有简洁快速,为最优解法
方法三利用零点分区间转化为分段函数利用函数单调性求![]() 最小值,要注意函数
最小值,要注意函数![]() 中的各绝对值的零点的大小关系,采用分类讨论方法,使用与更广泛的情况;
中的各绝对值的零点的大小关系,采用分类讨论方法,使用与更广泛的情况;
方法四与方法一的不同在于得到函数![]() 的最小值后,构造关于
的最小值后,构造关于![]() 的函数,利用数形结合思想求解关于
的函数,利用数形结合思想求解关于![]() 的不等式.
的不等式.
【2020年新课标1卷理科】
5.已知函数![]() .
.
(1)画出![]() 的图像;
的图像;
(2)求不等式![]() 的解集.
的解集.
【答案】(1)详解解析;(2)![]() .
.
【分析】(1)根据分段讨论法,即可写出函数![]() 的解析式,作出图象;
的解析式,作出图象;
(2)作出函数![]() 的图象,根据图象即可解出.
的图象,根据图象即可解出.
【详解】(1)因为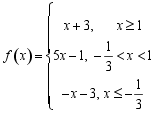 ,作出图象,如图所示:
,作出图象,如图所示: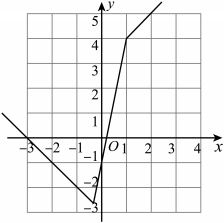
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,可得函数
个单位,可得函数![]() 的图象,如图所示:
的图象,如图所示:
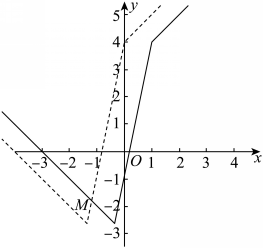
由![]() ,解得
,解得![]() .
.
所以不等式![]() 的解集为
的解集为![]() .
.
【点睛】本题主要考查画分段函数的图象,以及利用图象解不等式,意在考查学生的数形结合能力,属于基础题.
【2020年新课标2卷理科】
6.已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【分析】(1)分别在![]() 、
、![]() 和
和![]() 三种情况下解不等式求得结果;
三种情况下解不等式求得结果;
(2)利用绝对值三角不等式可得到![]() ,由此构造不等式求得结果.
,由此构造不等式求得结果.
【详解】(1)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
综上所述:![]() 的解集为
的解集为![]() 或
或![]() .
.
(2)![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 的取值范围为
的取值范围为![]() .
.
【点睛】本题考查绝对值不等式的求解、利用绝对值三角不等式求解最值的问题,属于常考题型.
【2020年新课标3卷理科】
7.设a,b,c![]() R,a+b+c=0,abc=1.
R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥![]() .
.
【答案】(1)证明见解析(2)证明见解析.
【分析】(1)方法一:由![]() 结合不等式的性质,即可得出证明;
结合不等式的性质,即可得出证明;
(2)方法一:不妨设![]() ,因为
,因为![]() ,所以
,所以![]()
![]()
![]()
![]() ,则
,则![]()
![]() .故原不等式成立.
.故原不等式成立.
【详解】(1)[方法一]【最优解】:通性通法
![]() ,
,
![]() .
.
![]() 均不为
均不为![]() ,则
,则![]() ,
,![]() .
.
[方法二]:消元法
由![]() 得
得![]() ,则
,则![]()
![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又![]() ,所以
,所以![]() .
.
[方法三]:放缩法
方式1:由题意知![]()
![]()
![]()
![]() ,又
,又![]()
![]()
![]()
![]() ,故结论得证.
,故结论得证.
方式2:因为![]() ,
,
所以![]()
![]()
![]() .
.
即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又![]() ,所以
,所以![]() .
.
[方法四]:
因为![]() ,所以a,b,c必有两个负数和一个正数,
,所以a,b,c必有两个负数和一个正数,
不妨设![]() 则
则![]()
![]() .
.
[方法五]:利用函数的性质
方式1:![]() ,令
,令![]() ,
,
二次函数对应的图像开口向下,又![]() ,所以
,所以![]() ,
,
判别式![]() ,无根,
,无根,
所以![]() ,即
,即![]() .
.
方式2:设![]() ,
,
则![]() 有a,b,c三个零点,若
有a,b,c三个零点,若![]() ,
,
则![]() 为R上的增函数,不可能有三个零点,
为R上的增函数,不可能有三个零点,
所以![]() .
.
(2)[方法一]【最优解】:通性通法
不妨设![]() ,因为
,因为![]() ,所以
,所以![]()
![]()
![]()
![]() ,
,
则![]() .故原不等式成立.
.故原不等式成立.
[方法二]:
不妨设![]() ,因为
,因为![]() ,所以
,所以![]() ,且
,且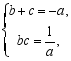
则关于x的方程![]() 有两根,其判别式
有两根,其判别式![]() ,即
,即![]() .
.
故原不等式成立.
[方法三]:
不妨设![]() ,则
,则![]()
![]()
![]()
![]()
![]() ,关于c的方程有解,判别式
,关于c的方程有解,判别式![]() ,则
,则![]() .故原不等式成立.
.故原不等式成立.
[方法四]:反证法
假设![]() ,不妨令
,不妨令![]() ,则
,则![]()
![]() ,又
,又![]() ,矛盾,故假设不成立.即
,矛盾,故假设不成立.即![]() ,命题得证.
,命题得证.
【整体点评】(1)方法一:利用三项平方和的展开公式结合非零平方为正数即可证出,证法常规,为本题的通性通法,也是最优解法;方法二:利用消元法结合一元二次函数的性质即可证出;方法三:利用放缩法证出;方法四:利用符号法则结合不等式性质即可证出;方法五:利用函数的性质证出.
(2)方法一:利用基本不等式直接证出,是本题的通性通法,也是最优解;
方法二:利用一元二次方程根与系数的关系以及方程有解的条件即可证出;方法三:利用消元法以及一元二次方程有解的条件即可证出;方法四:利用反证法以及基本不等式即可证出.
试卷第1页,共3页